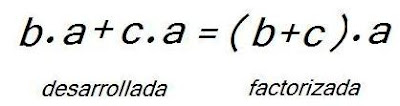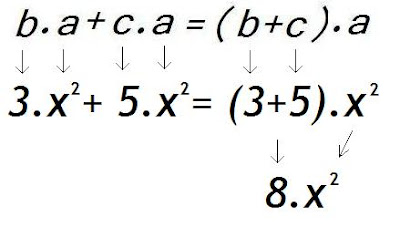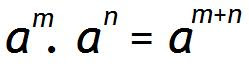El hombre que calculaba.

Cuenta la leyenda que al llegar el gran calculador Beremiz a la posada del viejo Salim, éste le planteó el siguiente problema:

- Un joyero que vino para vender sus joyas me prometió que me pagaría por el hospedaje 20 dinares si vendía sus joyas por 100 dinares y 35 si lograba venderlas por 200 dinares. Al cabo de unos días acabó vendiéndolas por 140 dinares, y por tanto debe pagarme 28 dinares, pero el joyero solo quiere pagarme 24,5.

- ¿Qué razonamiento hicieron Salim y el joyero para llegar cada uno a su solución?

- ¿Cuánto debería pagar en realidad por el hospedaje, de acuerdo con el trato establecido?

Lectura e interpretación de gráficos.

Hola, jóvenes, estoy corrigiendo las pruebas y en esta semana espero poder comunicarles los resultados.

Dejo unos ejercicios para insistir en el tema de la interpretación de gráficos. La idea es imprimir, recortar y pegar en el cuaderno los ejercicios a medida que los van haciendo. Los discutimos en clase.

FUNCIONES - Cortes con los ejes.

ECUACIONES de primer grado con 1 incógnita.

Aqui les dejo un repartido con ejercicios de ecuaciones para que se practiquen.

Recuerden que lo más importante en esta etapa es plantear paso por paso y de arriba hacia abajo cada transformación que se realiza al resolverlas.

ejercicios_ecuaciones1

Funciones Lineales y Afines.

Un estanque tiene un grifo que vierte 5 litros por minuto.
Consideremos los siguientes casos:

1) Si el volumen inicial del estanque fuera 0 litros:

2) Si el volumen inicial fuera de 20 litros.

a) Copia y completa la siguiente tabla de correspondencias.

Escribe en el último renglón las fórmulas correspondientes para un tiempo cualquiera llamado t.

b) Representa graficamente las dos funciones en un mismo sistema de coordenadas cartesiano. ¿Qué observas?


Ejercicios parecidos a este puedes encontrar aquí.

Aquí algunos cuadernos luego de trabajar con la actividad. Nos faltó escribir las conclusiones a las que llegamos. Seguimos en la próxima clase. Recuerden que la idea es investigar semejanzas y diferencias entre los dos tipos de funciones: la función lineal y la función afín.

Espero y deseo que este curso les esté siendo provechoso en sumo grado; ahora toca un poco de descanso para ustedes y si les ha quedado alguna asignatura para septiembre, a trabajar en cuanto sea posible. Si les surge alguna duda, usen este blog para preguntármela, por favor.

Es un placer tenerles como alumnos. Felices vacaciones.

Mediatrices y circuncentro

PUNTOS NOTABLES EN UN TRIÁNGULO.Se llaman puntos notables del triángulo a los puntos de intersección de las alturas, de las mediatrices, de las bisectrices y de las medianas, respectivamente.
Los estudiaremos uno por uno.





Recuerda que la mediatriz de un segmento es la recta perpendicular al mismo por su punto medio.
Antes de seguir repasemos la propiedad de la mediatriz de un segmento.


PROPIEDAD DE LA MEDIATRIZ
Todos los puntos pertenecientes a la mediatriz de un segmento están a la misma distancia de los extremos del mismo.
En la figura de abajo aparece un segmento AB y su mediatriz. Mueve el punto P perteneciente a la mediatriz de AB para investigar distintas posiciones.

Lo siento, GeoGebra Applet no puede iniciar. Asegúrese que tiene Java 1.4.2 (o posterior) instalado y activelo en su explorador (Clic aquí para instalar Java ahora)

Cada lado del triángulo, por ser un segmento, tendrá su correspondiente mediatriz. Es decir que én un triángulo se pueden trazar 3 mediatrices.
Si consideramos un triángulo ABC cualquiera y trazamos las mediatrices de sus tres lados, podemos observar que las tres mediatrices se cortan en un mismo punto.
Ese punto se llama circuncentro del triángulo.

Lo siento, GeoGebra Applet no puede iniciar. Asegúrese que tiene Java 1.4.2 (o posterior) instalado y activelo en su explorador (Clic aquí para instalar Java ahora)

PROPIEDAD DEL CIRCUNCENTRO
Usando la propiedad que tiene la mediatriz de un segmento es posible demostrar la propiedad que tiene el circuncentro de un triángulo.

Usa el deslizador que se llama i de la figura de abajo para ver la demostración.

Lo siento, GeoGebra Applet no puede iniciar. Asegúrese que tiene Java 1.4.2 (o posterior) instalado y activelo en su explorador (Clic aquí para instalar Java ahora)

BIBLIOTECA DIGITAL

Para repasar y ampliar conocimientos puedes consultar el siguiente material.
Matem Cbu 02 TriÁngulos

Regularidades en geometría

1. SUMA DE ÁNGULOS INTERIORES DE UN TRIÁNGULO.

Observa la siguente figura.
A la izquierda aparece un triángulo con la medida de sus tres ángulos interiores.
A la derecha se han colocado los ángulos uno a continuación del otro.
Verifícalo moviendo los vértices del triángulo.

¿Qué observas con respecto a la suma de los tres ángulos?
Mueve los vértices y verifica si tu conjetura se cumple para cualquier tipo de triángulo.

Lo siento, GeoGebra Applet no puede iniciar. Asegúrese que tiene Java 1.4.2 (o posterior) instalado y activelo en su explorador (Clic aquí para instalar Java ahora)

2. SUMA DE ÁNGULOS INTERIORES DE UN CUADRILÁTERO.

¿Y qué ocurre con la suma de los ángulos interiores de los cuadriláteros?
Investiga con la figura y dedúcelo tu mismo.

Lo siento, GeoGebra Applet no puede iniciar. Asegúrese que tiene Java 1.4.2 (o posterior) instalado y activelo en su explorador (Clic aquí para instalar Java ahora)

3. SUMA DE ÁNGULOS INTERIORES DE UN PENTÁGONO.

Siguiendo el razonamiento anterior deduce cuanto suman los angulos interiores de un pentágono.

Lo siento, GeoGebra Applet no puede iniciar. Asegúrese que tiene Java 1.4.2 (o posterior) instalado y activelo en su explorador (Clic aquí para instalar Java ahora)

4. GENERALIZANDO

Encuentra una fórmula general que te permita calcular la suma de los ángulos interiores de un polígono cualquiera si se sabe cuantos lados tiene.
Por ejemplo: ¿Cuánto suman los ángulos interiores de un polígono de 12 lados?

Escribe un comentario con lo que has descubierto. Y poné tu nombre y grupo porque este comentario se califica!!

TRIÁNGULOS

Llamamos triángulo a los polígonos de tres lados, que quedan determinados por tres puntos no alineados que llamamos vértices.

Los vértices son los puntos de intersección de los lados y se denotan por letras mayúsculas. En la figura son A, B y C.
Los lados son segmentos y se denotan con la misma letra que el vértice opuesto pero en minúscula: en la figura son a, b y c.
Los ángulos se denotan con la misma letra que el vértice correspondiente.
Los tres elementos básicos de un triángulo son: lados, vértices y ángulos.


CLASIFICACIÓN DE TRIÁNGULOS.
Para clasificar los triángulos se pueden seguir dos criterios, sus lados o sus ángulos. Abajo se muestra un esquema de resumen.


PROPIEDAD IMPORTANTE.La suma de los tres ángulos interiores de un triángulo es 180°

REDUCIR, FACTORIZAR Y DESARROLLAR

Les dejo fotocopia del capítulo con el que trabajaremos estas semanas.
expalg_gauss2

Publish at Scribd or explore others:

CÁLCULO ALGEBRAICO

Hemos visto en las actividades anteriores que para representar diversas situaciones en las que los números varían o simplemente se desconoce su valor, se utilizan letras.

Hemos descubierto fórmulas combinando letras con números mediante las operaciones conocidas, en las que las letras representan números que hay que calcular (incógnitas) o números que pueden tomar muchos valores (variables).

Este tipo de expresiones se llaman expresiones algebráicas o expresiones literales.

Ahora veremos cómo se realizan los cálculos cuando trabajamos con expresiones algebráicas. Es decir, cómo se realizan las operaciones que conocemos cuando trabajamos con expresiones algebráicas y no solamente con números.

Previamente debemos conocer algunos “nombres” que se usan con frecuencia. Lee la hoja que sigue y realiza las actividades planteadas.
monomios

Publish at Scribd or explore others:

PROPIEDAD DISTRIBUTIVA
En este momento es fundamental que repases la propiedad distributiva. Se utiliza con bastante frecuencia en el cálculo algebráico.


O también podemos escribirla de esta manera:

Porque la multiplicación cumple con la propiedad conmutativa, aquella que dice que el orden de los factores no altera el producto, la recuerdas?




Observa cómo se usa esta propiedad para SUMAR o RESTAR monomios semejantes.


Recuerda que solamente se pueden sumar o restar monomios que sean semejantes. Porque, justamente, al tener idéntica parte literal, es posible tomarla como factor común.




Para multiplicar monomios no es necesario que sean semejantes. La multiplicación se puede hacer siempre.
Es importante que recuerdes las propiedades de la multiplicación de potencias de la misma base.





LA PROPIEDAD DISTRIBUTIVA AMPLIADA.
Observa ahora esta situación:
Nuestro rectángulo está partido en cuatro. Mueve los puntos rojos y observa las expresiones escritas abajo de la figura.

Lo siento, GeoGebra Applet no puede iniciar. Asegúrese que tiene Java 1.4.2 (o posterior) instalado y activelo en su explorador (Clic aquí para instalar Java ahora)

¿Cómo escribirías con símbolos esta propiedad?

Problema del escrito RESUELTO

PROBLEMA.

Observa la secuencia de figuras construídas con palitos de la misma longitud.


a) Dibuja las dos figuras que siguen.
b) ¿Cuántos palitos se precisan para construirlas? A cada una, porsupu.
c) ¿Cuántos palitos se necesitan para construir la figura que ocupa el lugar N° 10?
d) ¿Y para construir la figura N° 123?
e) Escribe con palabras una regla que te permita calcular el número de palitos si se conoce el número de la figura.
-------------------- o ----------------------

A continuación les muestro algunas soluciones que realizaron los estudiantes.
Están muy buenas. ¡Felicitaciones!


PRIMERA SOLUCIÓN




SEGUNDA FORMA DE RESOLVERLO

Problema resuelto

CUADRADOS Y PALITOS


------------------------------------------------------------------------------------
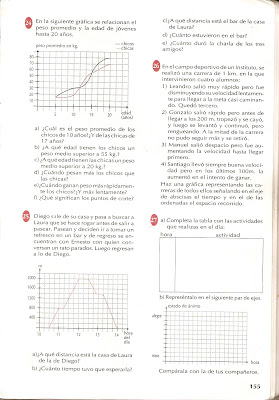
Observa la secuencia de figuras que aparece abajo.


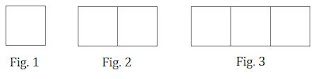
1) Dibuja las dos figuras que siguen en la secuencia.

2) Calcula la cantidad de palitos que se necesitan para dibujar la figura N° 10

3) Observando alguna regularidad, calcula los palitos necesarios para dibujar la figura que ocuupa el lugar 100 de esa secuencia.

4)Si le llamamos n al número de figura, escribe una fórmula que permita calcular los palitos en función de n.

-------------------------------------------------------------------------------------

SOLUCIONES POSIBLES

Las forma en que contaron los palitos determinó dos soluciones distintas pero que resultaron ser dos formas distintas de escribir la misma fórmula. Observa...

En la figura que aparecen abajo, arrastra el deslizador y fíjate cómo sigue la secuencia.

Lo siento, GeoGebra Applet no puede iniciar. Asegúrese que tiene Java 1.4.2 (o posterior) instalado y activelo en su explorador (Clic aquí para instalar Java ahora)

Este compañero, contó de la siguiente manera:

Cuatro palitos para la primera figura y luego agregó tres palitos para cada una de las figuras siguientes.

Mueve el deslizador para confirmarlo. Se han pintado de distinto color los palitos que se van agregando figura a figura.

Observa si existe alguna relación entre la cantidad que se suma 3 y el número de la figura en cada caso. Para verlo más claro, es conveniente completar una tabla como la que sigue. Recuerda dejar planteadas las operaciones.


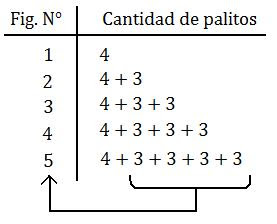
¡¡¡La cantidad de veces que se suma 3 es uno menos que el número de la figura!!!

Es decir que:

Cant. de palitos = 4 + 3.(número de figura menos 1)

Si le llamamos n al número de figura y p a la cantidad de palitos, entonces, a 4 hay que sumarle (n - 1) veces 3.
La fórmula en este caso es:


OTRA FORMA DE CONTAR PALITOS
Que dio lugar a otra fórmula. Observa...

Lo siento, GeoGebra Applet no puede iniciar. Asegúrese que tiene Java 1.4.2 (o posterior) instalado y activelo en su explorador (Clic aquí para instalar Java ahora)

Este compañero propone contar los palitos así:

Tres palitos para cada figura más un palito al final para cerrar.

Con lo que la fórmula en este caso queda:

ESTATUTO DEL ESTUDIANTE

ACTA Nº 47 – RESOLUCIÓN N° 2 del CODICEN

Les recomiendo que lean el Capítulo VI, que describe al Consejo Asesor Pedagógico (C.A.P.). Recuerden que en pocos días deberán elegir a su representante!!!
Las primeras cinco hojas son la circular firmada por el CODICEN y luego empieza el Estatuto. Les dejo un resumen de los capítulos para facilitar su lectura.

CAPÍTULO 1 – Principios generales - Artículos desde 1 hasta 9

CAPÍTULO 2 - Del ámbito subjetivo de aplicación – Artículo 10

CAPÍTULO 3 - De las carteleras y reuniones en centros de estudio – Artículos desde 11 hasta 13

CAPÍTULO 4 - Responsabilidades del educando – Artículos desde 14 hasta 18

CAPÍTULO 5 - De las Responsabilidades de los funcionarios, incluida la atinente a la aplicación de este Estatuto – Artículos 19

CAPÍTULO 6 - Del Consejo Asesor Pedagógico – Artículos desde 20 hasta 22

CAPÍTULO 7 - Del procedimiento disciplinario – Artículos desde 23 hasta 30

CAPÍTULO 8 - De las medidas correctivas – Artículos desde 31 hasta 36

CAPÍTULO 9 - Disposiciones transitorias – Artículos 37 y 38.
Estatuto Del Estudiante

Publish at Scribd or explore others:

PITÁGORAS Y EL PATO DONALD

En este videito de Walt Disney se cuenta la historia de Pitágoras y los pitagóricos.
Son muchas las contribuciones que hizo la secta pitagórica a la matemática y aunque ustedes no lo crean, a la música también. Si miran este video sería bueno que se lo comenten a la profe de música, seguro le va a gustar.

I made this video playlist at myflashfetish.com

TEOREMA DE PITÁGORAS

El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.


Demostración visual
Mueve el deslizador que aparece en la figura y justifica cada paso.


















Lo siento, GeoGebra Applet no puede iniciar. Asegúrese que tiene Java 1.4.2 (o posterior) instalado y activelo en su explorador (Clic aquí para instalar Java ahora)

Descubriendo regularidades.

REPARTIDO DE PROBLEMAS N°2
Les dejo, abajo, tres problemas que resolverán en clase esta semana.
También los dejo en la fotocopiadora. Para imprimirlo directo del blog hagan clic en el botón que dice "MORE" y buscan la opción para imprimir.


generalizacion1

En la entrada Matemática Segundo año: Problema resuelto está resuelto el problema N°1.

Potencias

PARA ESTUDIAR
GUIA POTENCIA

Publish at Scribd or explore others:

POTENCIAS DE 10
UN VIDEITO EXPLICATIVO
Potencias de diez es uno de los videos científicos más famosos de la historia. Powers of ten significa «potencias de diez» y es un video maravilloso. Primero nos alejamos de un bucólico picnic veraniego en saltos de potencias de diez: un metro, diez metros, cien metros, mil metros, hasta que nuestra galaxia desaparece en la lejanía; después nos acercamos en saltos de potencias de diez, hasta llegar al mundo subatómico. El video fue creado en 1977 y las imágenes solas son suficientes para entender el concepto.

Espero que lo hayas disfrutado, entiendes ahora por qué se llama POTENCIA esa operación que consiste en multiplicar un número, llamado BASE, por si mismo tantas veces como indique el EXPONENTE?

PARA ESTUDIAR
Lee el material copiado debajo y realiza los ejercicios planteados. Si tienes alguna pregunta que formular o alguna duda en concreto en la que te pueda ayudar, escríbela como comentario y la responderé.

Matem Cbu 05 Potencias

Publish at Scribd or explore others: Study Guides Academic Work potencia potencias

EJERCICIOS Aqui algunos problemas en los que se trabaja con potencias.

regularidades_potencias

Publish at Scribd or explore others: Academic Work Study Guides potencia potencias

Historia de los números

La historia del 1
Recuerdan el primer videito? El que estaba en portugués y contaba la historia de los números y la matemática. Bien, ese fue el primer capítulo de un total de siete.

Por fin encontré una versión en castellano!!!

Además está completa, media hora de cine...apaguen las luces! Si la quieres ver en pantalla completa debes hacer click en la región de la pantalla que dice "youtube".

I made this video playlist at myflashfetish.com

En el capítulo 2 se cuenta cómo los babilónicos inventaron una forma de escribir los números. Alrededor del año 1200 antes de Cristo.
Lo hacían sobre planchas de arcilla para que perdurara. Incluso tallaban piedras como se puede ver en las imagenes que gentilmente nos ha cedido el Museo del Louvre y El Museo de Irak.

Los símbolos que usaban para representar los números del 1 al 59 eran los que se muestran a continuación. Trata de encontrarlos en la piedra!

Inverso de un número - DIVISIÓN

¿Todos los números tienen inverso? ¿Existe algún número que multiplicado por 0 de 1? ¿Por qué?

Recuerda que llamamos números racionales a los que se pueden escribir como una fracción. ¿Cómo queda el inverso de un número racional?

Todo número de la forma salvo el cero, admite un inverso de la forma

Copia en tu cuaderno y completa la siguiente tabla:



En la figura de abajo aparecen representados dos números en una recta numérica. Uno es el inverso del otro.
Moviendo el punto que se llama "número" contesta las preguntas de más abajo.

Lo siento, GeoGebra Applet no puede iniciar. Asegúrese que tiene Java 1.4.2 (o posterior) instalado y activelo en su explorador (Clic aquí para instalar Java ahora)

1) A medida que el número aumenta, ¿qué ocurre con su inverso?

2) ¿Cuál es el inverso de 1?

3) Entre qué dos números se encuentran todos los inversos de los números mayores que 1?

4) ¿Cuál es el inverso de (-2)? ¿Por qué?

5) ¿Qué ocurre con los inversos de los números que están entre el 0 y el 1?

6) ¿Cómo son los signos de dos números opuestos?

Multiplicación y división con números negativos

Recuerda que cuando trabajamos con números naturales definimos a la multiplicación como una adición en la que todos los sumandos son iguales.




Veamos como extender este razonamiento a los números que tienen signos.
Primero veamos que si los sumandos son números negativos sería:

Observa que, en este caso, los FACTORES tienen signos distintos y el PRODUCTO queda con signo NEGATIVO.

En base a los dos ejemplos anteriores podemos afirmar que:
- Si los factores son positivos, el producto es positivo.
- Si los factores tienen signos distintos el producto es negativo.

Pero, ¿qué ocurre si los dos factores son negativos?
Para investigarlo necesitamos de la SUSTRACCIÓN. Observa.

Si restamos (-3) cinco veces, podemos escribirlo como sigue:


Para realizar el cálculo del producto haremos todas esas sustracciones. Para simplificar el cálculo agregaremos un cero al principio. Recuerda que el cero es el neutro de la suma por lo que no afecta el resultado.

¡El producto de dos números negativos es un número positivo!!!

Podemos resumir los casos estudiados en el siguiente diagrama: