Hemos descubierto fórmulas combinando letras con números mediante las operaciones conocidas, en las que las letras representan números que hay que calcular (incógnitas) o números que pueden tomar muchos valores (variables).
Este tipo de expresiones se llaman expresiones algebráicas o expresiones literales.
Ahora veremos cómo se realizan los cálculos cuando trabajamos con expresiones algebráicas. Es decir, cómo se realizan las operaciones que conocemos cuando trabajamos con expresiones algebráicas y no solamente con números.
Previamente debemos conocer algunos “nombres” que se usan con frecuencia. Lee la hoja que sigue y realiza las actividades planteadas.
monomios
Publish at Scribd or explore others:
PROPIEDAD DISTRIBUTIVA
En este momento es fundamental que repases la propiedad distributiva. Se utiliza con bastante frecuencia en el cálculo algebráico.

O también podemos escribirla de esta manera:
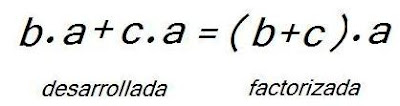
Porque la multiplicación cumple con la propiedad conmutativa, aquella que dice que el orden de los factores no altera el producto, la recuerdas?
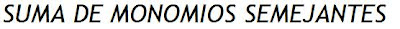
Observa cómo se usa esta propiedad para SUMAR o RESTAR monomios semejantes.
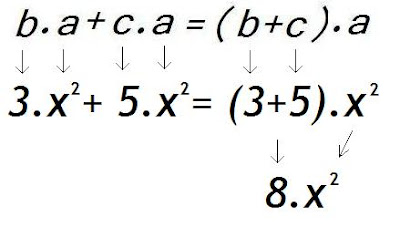
Recuerda que solamente se pueden sumar o restar monomios que sean semejantes. Porque, justamente, al tener idéntica parte literal, es posible tomarla como factor común.
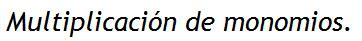
Para multiplicar monomios no es necesario que sean semejantes. La multiplicación se puede hacer siempre.
Es importante que recuerdes las propiedades de la multiplicación de potencias de la misma base.
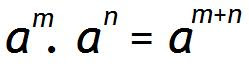
LA PROPIEDAD DISTRIBUTIVA AMPLIADA.
Observa ahora esta situación:
Nuestro rectángulo está partido en cuatro. Mueve los puntos rojos y observa las expresiones escritas abajo de la figura.
¿Cómo escribirías con símbolos esta propiedad?

